Altitude (triangle)

In geometry, an altitude of a triangle is a line segment through a given vertex (called apex) and perpendicular to a line containing the side or edge opposite the apex. This (finite) edge and (infinite) line extension are called, respectively, the base and extended base of the altitude. The point at the intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude" or "height", symbol h, is the distance between the foot and the apex. The process of drawing the altitude from a vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.
Altitudes can be used in the computation of the area of a triangle: one-half of the product of an altitude's length and its base's length (symbol b) equals the triangle's area: A=hb/2. Thus, the longest altitude is perpendicular to the shortest side of the triangle. The altitudes are also related to the sides of the triangle through the trigonometric functions.
In an isosceles triangle (a triangle with two congruent sides), the altitude having the incongruent side as its base will have the midpoint of that side as its foot. Also the altitude having the incongruent side as its base will be the angle bisector of the vertex angle.
In a right triangle, the altitude drawn to the hypotenuse c divides the hypotenuse into two segments of lengths p and q. If we denote the length of the altitude by hc, we then have the relation

For acute triangles, the feet of the altitudes all fall on the triangle's sides (not extended). In an obtuse triangle (one with an obtuse angle), the foot of the altitude to the obtuse-angled vertex falls in the interior of the opposite side, but the feet of the altitudes to the acute-angled vertices fall on the opposite extended side, exterior to the triangle. This is illustrated in the adjacent diagram: in this obtuse triangle, an altitude dropped perpendicularly from the top vertex, which has an acute angle, intersects the extended horizontal side outside the triangle.
Theorems
[edit]Orthocenter
[edit]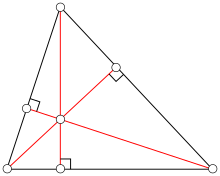
Altitude in terms of the sides
[edit]For any triangle with sides a, b, c and semiperimeter the altitude from side a (the base) is given by
This follows from combining Heron's formula for the area of a triangle in terms of the sides with the area formula where the base is taken as side a and the height is the altitude from the vertex A (opposite side a).
By exchanging a with b or c, this equation can also used to find the altitudes hb and hc, respectively.
Inradius theorems
[edit]Consider an arbitrary triangle with sides a, b, c and with corresponding altitudes ha, hb, hc. The altitudes and the incircle radius r are related by[3]: Lemma 1
Circumradius theorem
[edit]Denoting the altitude from one side of a triangle as ha, the other two sides as b and c, and the triangle's circumradius (radius of the triangle's circumscribed circle) as R, the altitude is given by[4]
Interior point
[edit]If p1, p2, p3 are the perpendicular distances from any point P to the sides, and h1, h2, h3 are the altitudes to the respective sides, then[5]
Area theorem
[edit]Denoting the altitudes of any triangle from sides a, b, c respectively as ha, hb, hc, and denoting the semi-sum of the reciprocals of the altitudes as we have[6]
General point on an altitude
[edit]If E is any point on an altitude AD of any triangle △ABC, then[7]: 77–78
Triangle inequality
[edit]Since the area of the triangle is , the triangle inequality implies[8]
- .
Special cases
[edit]Equilateral triangle
[edit]From any point P within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. This is Viviani's theorem.
Right triangle
[edit]

In a right triangle with legs a and b and hypotenuse c, each of the legs is also an altitude: and . The third altitude can be found by the relation[9][10]
This is also known as the inverse Pythagorean theorem.
Note in particular:
See also
[edit]Notes
[edit]- ^ Smart 1998, p. 156
- ^ a b Berele & Goldman 2001, p. 118
- ^ Dorin Andrica and Dan S ̧tefan Marinescu. "New Interpolation Inequalities to Euler's R ≥ 2r". Forum Geometricorum, Volume 17 (2017), pp. 149–156. http://forumgeom.fau.edu/FG2017volume17/FG201719.pdf
- ^ Johnson 2007, p. 71, Section 101a
- ^ Johnson 2007, p. 74, Section 103c
- ^ Mitchell, Douglas W., "A Heron-type formula for the reciprocal area of a triangle," Mathematical Gazette 89, November 2005, 494.
- ^ Alfred S. Posamentier and Charles T. Salkind, Challenging Problems in Geometry, Dover Publishing Co., second revised edition, 1996.
- ^ Mitchell, Douglas W., "A Heron-type formula for the reciprocal area of a triangle", Mathematical Gazette 89 (November 2005), 494.
- ^ Voles, Roger, "Integer solutions of ," Mathematical Gazette 83, July 1999, 269–271.
- ^ Richinick, Jennifer, "The upside-down Pythagorean Theorem," Mathematical Gazette 92, July 2008, 313–317.
References
[edit]- Altshiller-Court, Nathan (2007) [1952], College Geometry, Dover
- Berele, Allan; Goldman, Jerry (2001), Geometry: Theorems and Constructions, Prentice Hall, ISBN 0-13-087121-4
- Bogomolny, Alexander. "Existence of the Orthocenter". Cut the Knot. Retrieved 2022-12-17.
- Johnson, Roger A. (2007) [1960], Advanced Euclidean Geometry, Dover, ISBN 978-0-486-46237-0
- Smart, James R. (1998), Modern Geometries (5th ed.), Brooks/Cole, ISBN 0-534-35188-3


















![{\displaystyle {\begin{aligned}{\tfrac {1}{2}}AC\cdot BC&={\tfrac {1}{2}}AB\cdot CD\\[4pt]CD&={\tfrac {AC\cdot BC}{AB}}\\[4pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3568e8b4c2f2792d3e08b8f06654c6530eab06cb)
